之前有过两期内容，都是讲已知一个圆如何去寻找它的圆心或确定它的半径。在《》这一期中，介绍了三种办法，是既可以用直尺也可以用圆规。而在《》这一期中，讲了只用圆规的方法。本期再讲一种方法，也是只用圆规，就可以找到圆心。

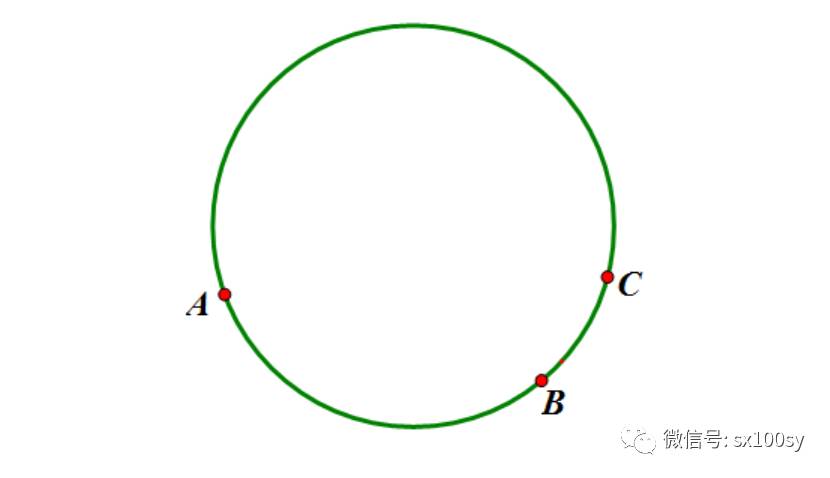
如下图所示，有一个圆，我们怎么求它的圆心？图中给出了圆上的三个点。因为在圆上取点是任意的，所以，本问题也可以说成是已知一个圆及圆上任意三点，求作这个圆的圆心。要求只用圆规。

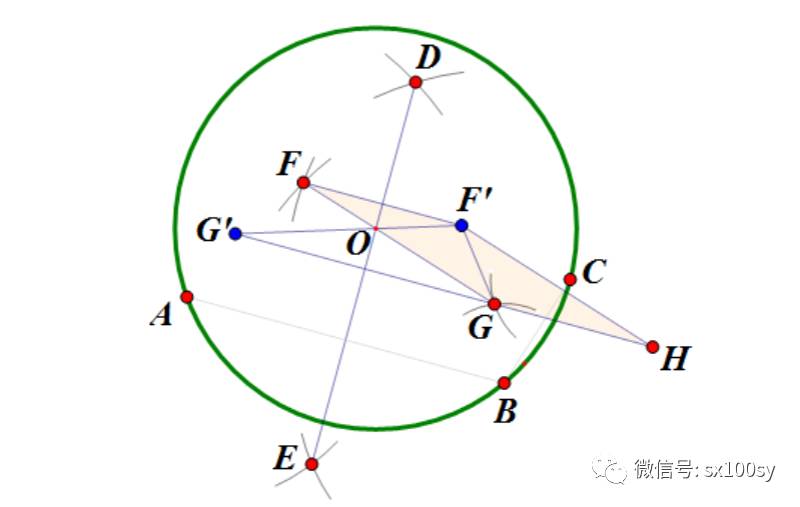
（1）如下图所示，我们可以只用圆规作出AB中垂线上的两个点D和E，也可以作出BC中垂线上的两个点F和G。

（2）只用圆规也很容易作出点F和G关于中垂线DE的对称点F'和G'。（其实，FG和F'G'的交点一定是圆心，只是我们不能用直尺连线， 我们心须用圆规作出圆心。）

（3）作一个平行四边形FGHF'，其中三个顶点为已作出的点F，G和F'，而第四个顶点是与点F相对的顶点（只用圆规可以做到）。于是有三角形G'GO与三角形G'HF'相似，所以有G'H/G'G=F'H/OG。从图中可以看出，G'H，G'G，F'H这三条线段的长度是确定的，我们只要作出一线段，它的长度等于OG即可（其实只要线段的两个端点确定下来即可）。然后就可以分别以G'和G为圆心，以这个长度为半径作圆弧，两圆弧的交点之一就是圆心。所以，我们现在的问题就是如何作出这个长度。

（4）成比例的四条线段中，若三条是确定的，那么，我们是可以只用圆规作出第四条线段的（只要线段的两个端点确定了，就说这条线段是确定的。我们可以用圆规的两个脚分别对准线段的两个端点而取得这条线段的长度）。请看下面的步骤。

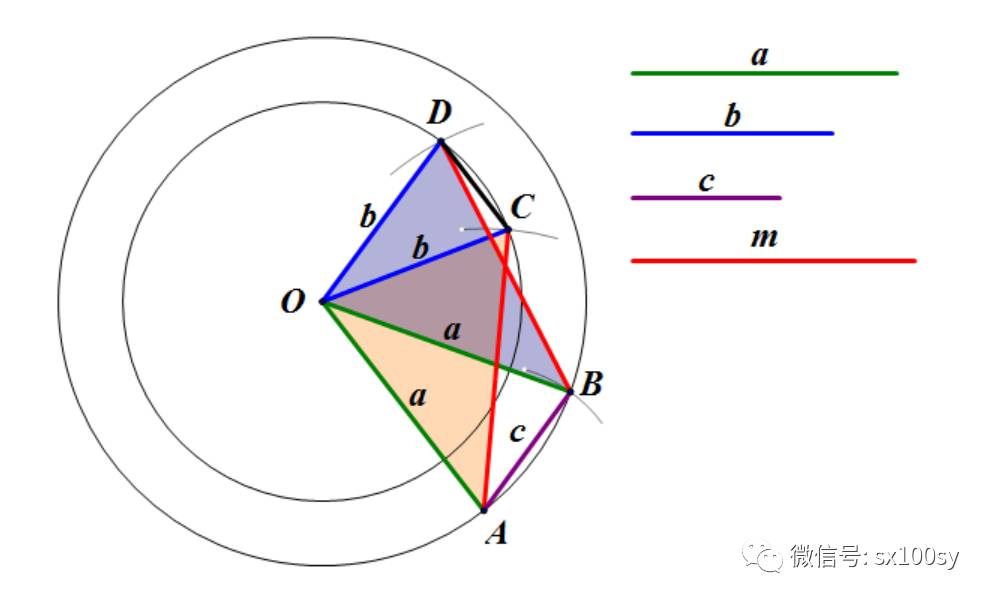
上图是这样作出来的：

（1）作半径分别等于a和b的同心圆O1和O2。在以a为半径的O1上取一点A，以A为圆心，c为半径作圆弧，在O1上交出点B。连接三角形OAB。

（2）分别以A和B为圆心，以任意长度m为半径作圆弧，分别与O2交于C和D。连接三角形OCD。

（3）再连接AC，连接BD。所以，三角形OAC和三角形OBD全等（边边边）。所以，角AOC=角BOD，所以，角AOB=角COD。由此得出两个等腰三角形OAB和OCD相似。因此，a：c = b：d（d为CD的长度）。d就是所求的成比例的四条线段中的第四条。

最后， 我们把上面的方法用于本问题。如下图所示，把G'H取为a，把G'G取作b，把F'H取作c，那么，求出的d就是OG的长度。于是，我们分别以G'和G为圆心，以d为半径作圆弧，那么，位于F和G之间的交点就是所求作的圆心O。